Zadania Godzio: Eta Masz może jakieś ciekawe zadanko, bo tych moich do szkoły już mi się nie chce robić

Eta: Witaj Godzio Poczekaj na Bogdana z pewnością coś ciekawego Ci podrzuci Ja narazie zmagam się z bólem głowy

lolly: Godzio − jak chcesz, rozwiąż moje , jak do tej pory nikt sie nie pokusił, co oznacza, że chyba jest na odpowiednim poziomie z pojemnika, w którym znajduje się 5 kul białych oraz 4 czarne losujemy trzy kule bez zwracania.oblicz prawdopodobieństwo wylosowania: a) dwóch kul białych c) co najmniej jednej kuli białej

Eta: Za łatwe

ewa: albo z moimi granicami https://matematykaszkolna.pl/forum/85151.html

lolly: dlaczego nikt tutaj nie lubi kombinatoryki, prawdopodobieństwa , wszelkich wariacji itp? ja może i bym lubiła (gdybym rozumiała)

lolly: jak za łatwe Eta? ja to nawet się nie wiem jak do tego zabrać, a jak się kogoś pytam , to słyszę tylko 'drzewko narysuj' a ja tych drzewek nie lubię rysować (zresztą nawet nie umiem: D )

zdesperowany student: moze skorzystaj ze strony zadania.info tam jest wiele ciekawych zadan

Eta: 5 b , 4 cz, R−m 9 kul

	9 3
|Ω|=		= ........

	5 2		4 1
a) |A|=		*		= ......

	|A|
P(A)=		=........
	|Ω|

c) C^' −−−− żadnej białej

	4 3
|C'|=		=......

P(C)= 1− P(C^')=........ dokończ obliczenia ..........

lolly: dziękuję bardzo Eta zaraz sobie wszystko przeanalizuję, może dojdę do tego, jak zrobić inne zadania z tego prawdopodobieństwa

Eta: I żadnych " drzewek" tylko kombinacje

patryk:

	9 3
moc Ω = C39 =		(losujemy 3 z 9, nieważne w jakiej kolejności wyciągniemy)

a) moc A = C²₅*C¹₄ (losujemy 2 z 5 białych i 1 z 4 czarnych) b) B' = wylosowanie wszystkich czarnych − B − zdarzenie przeciwne czyli wylosowanie co najmniej jednej białej. B' = C³₄ (losowanie 3 z 4 czarnych) P(B) = 1 − P(B') Powinno być dobrze

Godzio: No to czekam dalej

ewa: Godzio a może jednak zmierzysz się z ciągami? ;>

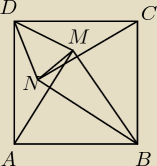
patryk: Na rozgrzewke: Wiedząc, że trójkąt ABM i BCN są równoboczne, udowodnij że trójkąt NMD też jest równoboczny.

Godzio: Musiałbym o tym chwilę poczytać, daj mi trochę czasu

Godzio: patryk to jest kwadrat ?

;): Godzio jezeli Cie interesuje to mam dla Ciebie takie zadanko trzeba obliczyc sume

	1		1		1
(2+		)2 + (4+		)2 + ... + (2n+		)2
	2		4		2n

patryk: Tak, ABCD jest kwadratem

Eta: He he dla Godzia .... to "pikuś"

Godzio: Dokładnie tydzień temu je robiłem podnoszę do kwadratu i zapisuje sumę odpowiednio 3 ciągów: 4 + 16 + ... + 2²ⁿ −− ciąg geometryczny o ilorazie q = 4

1		1		1		1
	+		+ ... +		−− ciąg geometryczny o ilorazie
4		16		22n		4

2 + 2 + ... + 2 = 2n Wystaczy zsumować i kóniec

;): Ee to nie wiedzialem ze juz robiles co to za przyjemnosc drugi raz to samo Jak znajde cos ciekawszego to dam znac

zdesperowany student: to moze takie zadanko dany jest ciag liczb 49,4489,444889,... kolejne liczby wyrazu ciagu powstaja poprzez dolaczenie liczby 48 w srodku poprzedniego. wykaz ze wszystkie wyrazy ciagu sa kwadratami pewnych liczb naturalnych.

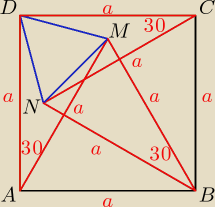
Godzio: Trójkąty AMD, DCN i BMN są przystające (b,k,b) więc boki DM, DN, MN są równe

patryk: Brawo, ja troszkę dłużej siedziałem przy tym żeby na to wpaść

Godzio: Lata praktyki , zabieram się za zadanie studenta

lolly: pytanko do ETY − powiedz mi tylko, co zrobiłam źle w tym zadanku z kulami, bo to C' wyszło mi 4, w takim razie p(c) wychodzi mi −3 Oo tak chyba nie może być, co? wiem, jestem matematycznie upośledzona : DD

zdesperowany student: powodzenia ja nad tym troche posiedzialem

Eta: @ lolly co też Ty wymyśliłaś?

	9 3		9!		6!*7*8*9
|Ω|=		=		=		= 84
			3!*61		1*2*3*6!

	4 3
|C'| =		= 4

	4		1
P(C')=		=
	84		21

	1		20
P(C)= 1− P(C')= 1 −		=
	21		21

lolly: hahaha a no tak, wiesz co ja zrobiłam? poprzestałam na C' = 4, a P(C') juz nie obliczyłam i to samotne C' podstawiłam do wzoru : )) to juz wiem, czemu mi tak wyszło dziękuję Ci bardzo za pomoc : ))

Eta:

	|C'|
P(C')=
	|Ω|

Godzio: 49, 4489, 444889 Oznaczam że jest n czwórek, n − 1 ósemek i 1 dziewiątka 10^{2n − 1} * 4 + ... + 10ⁿ * 4 + 10^{n − 1} * 8 + ... + 10 * 8 + 9 = 4 * (10^{2n − 1} + ... + 10ⁿ) + 8(10^{n − 1} + ... + 10) + 9

	1 − (1/10)n		1 − (1/10)n−1
4 * 102n−1*		+ 8*10n−1 *		+ 9 =
	9   10		9   10

4		1		8		1
	* 102n(1 − (		)n) +		* 10n * (1 − (		)n − 1) + 9 =
9		10		9		10

4
	( 102n − 10n + 2 * 10n − 2 * 10) + 9 =
9

4		1
	(102n + 10n − 20) + 9 =		(4 * 102n + 4 * 10n − 80 + 81) =
9		9

	1		1
=		(4 * 102n + 4 * 10n − 80 + 81) =		(4 * 102n + 4 * 10n + 1) =
	9		9

	1
= (		(2 * 102n + 1))2 Suma cyfr liczby 2 * 102n + 1 jest podzielna przez 3 więc
	3

liczba dzieli się przez 3, a za tym idzie że cała liczba jest naturalna więc jest to kwadrat liczby naturalnej uffffff dobrnąłem

Eta:

lolly: nie wiem, jak Wy wszyscy to robicie, ale jestem pełna podziwu tymczasem dobranoc, i jeszcze raz dzięki za pomoc

Godzio: Dobranoc

Eta: Miłych snów

zdesperowany student: i jak GODZIO zadanie?

zdesperowany student: sorry cos mi sie pomieszalo i nie wyswietlkilo napoczatku rozw

Godzio:

Vizer: Godzio Ty już jesteś po maturze czy przed? jeśli mogę wiedzieć

zdesperowany student: mozesz mi wystlumaczyc jak z tymi potegami tak doszedles bo nie rozumiem tego ja wyznaczylem to w inny sposob ale Twoj jest łatwiejszy

Godzio: Viser jestem przed maturą, zdesperowany Skoro jest 2n cyfr, a potęgi 10 zaczynają się od 0 (9 * 10⁰) to musi się to skończyć na 10²ⁿ I poprawka do zapisu bo nie zauważyłem:

	1
(		(2 * 10n + 1))2
	3

Basia zgoda tyle, że ja nie mówie że 49 dzieli się przez 3 tylko, że liczba 2 * 10ⁿ + 1 jest podzielna przez 3.

Basia: sorry już zauważyłam, że źle przeczytalam

Godzio: I znów "musi się skończyć na 10^{2n − 1} bo od 0 do 2n − 1 jest 2n cyfr

Basia: ignorujesz 49, bo jest oczywiste, że 49=7² i dla n≥2 masz 1 dziewiątka 1+1, 1+2, 1+3, ..........,1+n−1=n ósemki n+1, n+2,............n+n=2n czwórki wtedy skończysz na 2n i masz kłopot "z głowy"

zdesperowany student: to prosze kolejne zadanie rozw uklad rownan x^log_yz+z^log_yx=512 y^log_zx+x^log_zy=8 z^log_xy+y^log_xz=2√2

Godzio: Zostawie sobie to na jutro, trochę kosmiczne rachunki mi wychodzą

Basia: x,y,z>0; x,y,z≠1 a = log_xy ⇔ y = x^a b = log_xz ⇔ z = x^b c = log_yz ⇔ z = y^c = (x^a)^c = x^a*c = x^b a*c = b x^c+z^1/a = 512 x^c + x^b/a = 512 x^c + x^c = 512 2x^c = 512 x^c = 256= 2⁸ (x^a)^1/b+x^1/c = 8 x^a/b + x^1/c = 8 x^1/c+x^1/c = 8 x^1/c = 4=2² x^c = (x^1/c)⁴ x^c = x^4/c a to jest niemożliwe ⇔ c = ⁴_c ⇔ c² = 4 ⇔ c=2 lub c = −2 czyli log_yz = 2 lub log_yz = −2 z=y² lub z=y⁻² dalej powinno być już łatwo

Basia: tam oczywiście ma być: a to jest możliwe ⇔

....: ze zbioru cyfr 1 2 3 4 5 6 7 8 9 losujemy kolejno dwa razy po jednej cyfrze bez zwracania i zapisując wylosowane cyfry w kolejności losowania, otrzymujemy liczbę dwucyfrową. Oblicz prawdopodobieństwo otrzymania liczby: a) podzielnej przez pięć b) parzystej c) mniejszej od 63 d) większej od 36 proszę o wytłumaczenie